Answer
404.7k+ views
Hint: In this question, we need to construct a perpendicular bisector of the line PQ. For this, we will need a compass and ruler. First we will draw a line segment PQ = 4cm and then use the compass to draw arcs from both ends to both sides of the line. Then we will join points formed to get the perpendicular bisector. We will draw a perpendicular bisector step by step with written steps of construction.
Complete step-by-step answer:
Here, we need to draw a perpendicular bisector of the line PQ. Since PQ is given as 4cm. So following are the steps of construction involved in making a perpendicular bisector.
(i) Draw a line segment PQ = 4cm.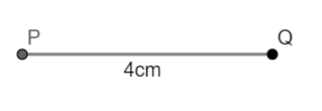
(ii) Now, open the compass more than half the length of the side PQ. With P as center and radius equal than half of PQ, draw an arc on both sides of PQ.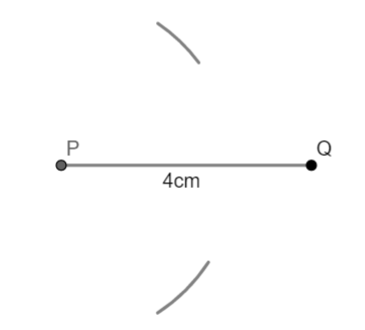
(iii) Now with Q as center and same radius as taken in 2, draw arcs on both sides of PQ. Let these arcs intersect each other at point A and B.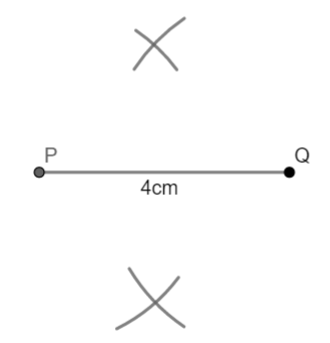
(iv) Join A and B. The line AB cuts the line segment PQ at the point O.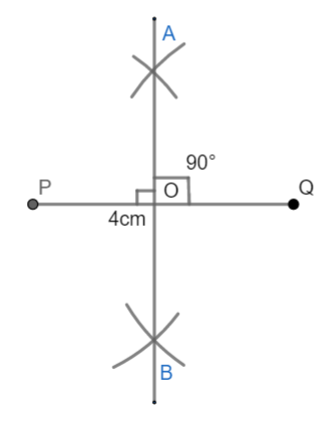
Here, OP = OQ and $\angle AOQ={{90}^{\circ }}$. Thus the line AB is a perpendicular bisector of AB.
Note: Students should note that the perpendicular bisector of any line is a line which cuts the line segments into two equal parts and is perpendicular to the line segment. While drawing arcs, make sure that the compass is opened more than half of PQ otherwise arcs will not cut. Students should check the final diagram seeing if OP = OQ and $\angle AOQ={{90}^{\circ }}$.
Complete step-by-step answer:
Here, we need to draw a perpendicular bisector of the line PQ. Since PQ is given as 4cm. So following are the steps of construction involved in making a perpendicular bisector.
(i) Draw a line segment PQ = 4cm.

(ii) Now, open the compass more than half the length of the side PQ. With P as center and radius equal than half of PQ, draw an arc on both sides of PQ.

(iii) Now with Q as center and same radius as taken in 2, draw arcs on both sides of PQ. Let these arcs intersect each other at point A and B.

(iv) Join A and B. The line AB cuts the line segment PQ at the point O.

Here, OP = OQ and $\angle AOQ={{90}^{\circ }}$. Thus the line AB is a perpendicular bisector of AB.
Note: Students should note that the perpendicular bisector of any line is a line which cuts the line segments into two equal parts and is perpendicular to the line segment. While drawing arcs, make sure that the compass is opened more than half of PQ otherwise arcs will not cut. Students should check the final diagram seeing if OP = OQ and $\angle AOQ={{90}^{\circ }}$.
Recently Updated Pages
How many sigma and pi bonds are present in HCequiv class 11 chemistry CBSE

Why Are Noble Gases NonReactive class 11 chemistry CBSE

Let X and Y be the sets of all positive divisors of class 11 maths CBSE

Let x and y be 2 real numbers which satisfy the equations class 11 maths CBSE

Let x 4log 2sqrt 9k 1 + 7 and y dfrac132log 2sqrt5 class 11 maths CBSE

Let x22ax+b20 and x22bx+a20 be two equations Then the class 11 maths CBSE

Trending doubts
Establish a relation between electric current and drift class 12 physics CBSE

Guru Purnima speech in English in 100 words class 7 english CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Difference Between Plant Cell and Animal Cell

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

Copper is not used as potentiometer wire because class 12 physics CBSE

Give 10 examples for herbs , shrubs , climbers , creepers

Fill in the blanks A 1 lakh ten thousand B 1 million class 9 maths CBSE







