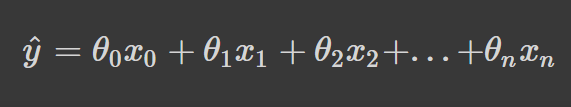Normal Equation is an analytical approach to Linear Regression with a Least Square Cost Function. We can directly find out the value of θ without using Gradient Descent. Following this approach is an effective and a time-saving option when are working with a dataset with small features.
Normal Equation is a follows :
In the above equation,
θ : hypothesis parameters that define it the best.
X : Input feature value of each instance.
Y : Output value of each instance.
Maths Behind the equation –
Given the hypothesis function
where,
n : the no. of features in the data set.
x0 : 1 (for vector multiplication)
Notice that this is dot product between θ and x values. So for the convenience to solve we can write it as :
The motive in Linear Regression is to minimize the cost function :
J(Theta) = frac{1}{2m} sum_{i = 1}^{m} frac{1}{2} [h_{Theta}(x^{(i)}) – y^{(i)}]^{2}
where,
xi : the input value of iih training example.
m : no. of training instances
n : no. of data-set features
yi : the expected result of ith instance
Let us representing cost function in a vector form.
we have ignored 1/2m here as it will not make any difference in the working. It was used for the mathematical convenience while calculation gradient descent. But it is no more needed here.
xij : value of jih feature in iih training example.
This can further be reduced to Xtheta – y
But each residual value is squared. We cannot simply square the above expression. As the square of a vector/matrix is not equal to the square of each of its values. So to get the squared value, multiply the vector/matrix with its transpose. So, the final equation derived is
Therefore, the cost function is
So, now getting the value of θ using derivative
So, this is the finally derived Normal Equation with θ giving the minimum cost value.