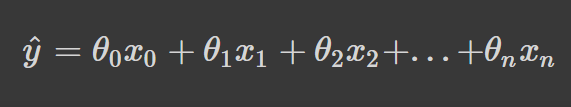I am doing linear regression with multiple variables/features. I try to get thetas (coefficients) by using normal equation method (that uses matrix inverse), Numpy least-squares numpy.linalg.lstsq tool and np.linalg.solve tool. In my data I have n = 143 features and m = 13000 training examples.
For normal equation method with regularization I use this formula:
Regularization is used to solve the potential problem of matrix non-invertibility (XtX matrix may become singular/non-invertible)
Data preparation code:
import pandas as pd
import numpy as np
path = 'DB2.csv'
data = pd.read_csv(path, header=None, delimiter=";")
data.insert(0, 'Ones', 1)
cols = data.shape[1]
X = data.iloc[:,0:cols-1]
y = data.iloc[:,cols-1:cols]
IdentitySize = X.shape[1]
IdentityMatrix= np.zeros((IdentitySize, IdentitySize))
np.fill_diagonal(IdentityMatrix, 1)
For least squares method I use Numpy’s numpy.linalg.lstsq. Here is Python code:
lamb = 1
th = np.linalg.lstsq(X.T.dot(X) + lamb * IdentityMatrix, X.T.dot(y))[0]
Also I used np.linalg.solve tool of numpy:
lamb = 1
XtX_lamb = X.T.dot(X) + lamb * IdentityMatrix
XtY = X.T.dot(y)
x = np.linalg.solve(XtX_lamb, XtY);
For normal equation I use:
lamb = 1
xTx = X.T.dot(X) + lamb * IdentityMatrix
XtX = np.linalg.inv(xTx)
XtX_xT = XtX.dot(X.T)
theta = XtX_xT.dot(y)
In all methods I used regularization. Here is results (theta coefficients) to see difference between these three approaches:
Normal equation: np.linalg.lstsq np.linalg.solve
[-27551.99918303] [-27551.95276154] [-27551.9991855]
[-940.27518383] [-940.27520138] [-940.27518383]
[-9332.54653964] [-9332.55448263] [-9332.54654461]
[-3149.02902071] [-3149.03496582] [-3149.02900965]
[-1863.25125909] [-1863.2631435] [-1863.25126344]
[-2779.91105618] [-2779.92175308] [-2779.91105347]
[-1226.60014026] [-1226.61033117] [-1226.60014192]
[-920.73334259] [-920.74331432] [-920.73334194]
[-6278.44238081] [-6278.45496955] [-6278.44237847]
[-2001.48544938] [-2001.49566981] [-2001.48545349]
[-715.79204971] [-715.79664124] [-715.79204921]
[ 4039.38847472] [ 4039.38302499] [ 4039.38847515]
[-2362.54853195] [-2362.55280478] [-2362.54853139]
[-12730.8039209] [-12730.80866036] [-12730.80392076]
[-24872.79868125] [-24872.80203459] [-24872.79867954]
[-3402.50791863] [-3402.5140501] [-3402.50793382]
[ 253.47894001] [ 253.47177732] [ 253.47892472]
[-5998.2045186] [-5998.20513905] [-5998.2045184]
[ 198.40560401] [ 198.4049081] [ 198.4056042]
[ 4368.97581411] [ 4368.97175688] [ 4368.97581426]
[-2885.68026222] [-2885.68154407] [-2885.68026205]
[ 1218.76602731] [ 1218.76562838] [ 1218.7660275]
[-1423.73583813] [-1423.7369068] [-1423.73583793]
[ 173.19125007] [ 173.19086525] [ 173.19125024]
[-3560.81709538] [-3560.81650156] [-3560.8170952]
[-142.68135768] [-142.68162508] [-142.6813575]
[-2010.89489111] [-2010.89601322] [-2010.89489092]
[-4463.64701238] [-4463.64742877] [-4463.64701219]
[ 17074.62997704] [ 17074.62974609] [ 17074.62997723]
[ 7917.75662561] [ 7917.75682048] [ 7917.75662578]
[-4234.16758492] [-4234.16847544] [-4234.16758474]
[-5500.10566329] [-5500.106558] [-5500.10566309]
[-5997.79002683] [-5997.7904842] [-5997.79002634]
[ 1376.42726683] [ 1376.42629704] [ 1376.42726705]
[ 6056.87496151] [ 6056.87452659] [ 6056.87496175]
[ 8149.0123667] [ 8149.01209157] [ 8149.01236827]
[-7273.3450484] [-7273.34480382] [-7273.34504827]
[-2010.61773247] [-2010.61839251] [-2010.61773225]
[-7917.81185096] [-7917.81223606] [-7917.81185084]
[ 8247.92773739] [ 8247.92774315] [ 8247.92773722]
[ 1267.25067823] [ 1267.24677734] [ 1267.25067832]
[ 2557.6208133] [ 2557.62126916] [ 2557.62081337]
[-5678.53744654] [-5678.53820798] [-5678.53744647]
[ 3406.41697822] [ 3406.42040997] [ 3406.41697836]
[-8371.23657044] [-8371.2361594] [-8371.23657035]
[ 15010.61728285] [ 15010.61598236] [ 15010.61728304]
[ 11006.21920273] [ 11006.21711213] [ 11006.21920284]
[-5930.93274062] [-5930.93237071] [-5930.93274048]
[-5232.84459862] [-5232.84557665] [-5232.84459848]
[ 3196.89304277] [ 3196.89414431] [ 3196.8930428]
[ 15298.53309912] [ 15298.53496877] [ 15298.53309919]
[ 4742.68631183] [ 4742.6862601] [ 4742.68631172]
[ 4423.14798495] [ 4423.14765013] [ 4423.14798546]
[-16153.50854089] [-16153.51038489] [-16153.50854123]
[-22071.50792741] [-22071.49808389] [-22071.50792408]
[-688.22903323] [-688.2310229] [-688.22904006]
[-1060.88119863] [-1060.8829114] [-1060.88120546]
[-101.75750066] [-101.75776411] [-101.75750831]
[ 4106.77311898] [ 4106.77128502] [ 4106.77311218]
[ 3482.99764601] [ 3482.99518758] [ 3482.99763924]
[-1100.42290509] [-1100.42166312] [-1100.4229119]
[ 20892.42685103] [ 20892.42487476] [ 20892.42684422]
[-5007.54075789] [-5007.54265501] [-5007.54076473]
[ 11111.83929421] [ 11111.83734144] [ 11111.83928704]
[ 9488.57342568] [ 9488.57158677] [ 9488.57341883]
[-2992.3070786] [-2992.29295891] [-2992.30708529]
[ 17810.57005982] [ 17810.56651223] [ 17810.57005457]
[-2154.47389712] [-2154.47504319] [-2154.47390285]
[-5324.34206726] [-5324.33913623] [-5324.34207293]
[-14981.89224345] [-14981.8965674] [-14981.89224973]
[-29440.90545197] [-29440.90465897] [-29440.90545704]
[-6925.31991443] [-6925.32123144] [-6925.31992383]
[ 104.98071593] [ 104.97886085] [ 104.98071152]
[-5184.94477582] [-5184.9447972] [-5184.94477792]
[ 1555.54536625] [ 1555.54254362] [ 1555.5453638]
[-402.62443474] [-402.62539068] [-402.62443718]
[ 17746.15769322] [ 17746.15458093] [ 17746.15769074]
[-5512.94925026] [-5512.94980649] [-5512.94925267]
[-2202.8589276] [-2202.86226244] [-2202.85893056]
[-5549.05250407] [-5549.05416936] [-5549.05250669]
[-1675.87329493] [-1675.87995809] [-1675.87329255]
[-5274.27756529] [-5274.28093377] [-5274.2775701]
[-5424.10246845] [-5424.10658526] [-5424.10247326]
[-1014.70864363] [-1014.71145066] [-1014.70864845]
[ 12936.59360437] [ 12936.59168749] [ 12936.59359954]
[ 2912.71566077] [ 2912.71282628] [ 2912.71565599]
[ 6489.36648506] [ 6489.36538259] [ 6489.36648021]
[ 12025.06991281] [ 12025.07040848] [ 12025.06990358]
[ 17026.57841531] [ 17026.56827742] [ 17026.57841044]
[ 2220.1852193] [ 2220.18531961] [ 2220.18521579]
[-2886.39219026] [-2886.39015388] [-2886.39219394]
[-18393.24573629] [-18393.25888463] [-18393.24573872]
[-17591.33051471] [-17591.32838012] [-17591.33051834]
[-3947.18545848] [-3947.17487999] [-3947.18546459]
[ 7707.05472816] [ 7707.05577227] [ 7707.0547217]
[ 4280.72039079] [ 4280.72338194] [ 4280.72038435]
[-3137.48835901] [-3137.48480197] [-3137.48836531]
[ 6693.47303443] [ 6693.46528167] [ 6693.47302811]
[-13936.14265517] [-13936.14329336] [-13936.14267094]
[ 2684.29594641] [ 2684.29859601] [ 2684.29594183]
[-2193.61036078] [-2193.63086307] [-2193.610366]
[-10139.10424848] [-10139.11905454] [-10139.10426049]
[ 4475.11569903] [ 4475.12288711] [ 4475.11569421]
[-3037.71857269] [-3037.72118246] [-3037.71857265]
[-5538.71349798] [-5538.71654224] [-5538.71349794]
[ 8008.38521357] [ 8008.39092739] [ 8008.38521361]
[-1433.43859633] [-1433.44181824] [-1433.43859629]
[ 4212.47144667] [ 4212.47368097] [ 4212.47144686]
[ 19688.24263706] [ 19688.2451694] [ 19688.2426368]
[ 104.13434091] [ 104.13434349] [ 104.13434091]
[-654.02451175] [-654.02493111] [-654.02451174]
[-2522.8642551] [-2522.88694451] [-2522.86424254]
[-5011.20385919] [-5011.22742915] [-5011.20384655]
[-13285.64644021] [-13285.66951459] [-13285.64642763]
[-4254.86406891] [-4254.88695873] [-4254.86405637]
[-2477.42063206] [-2477.43501057] [-2477.42061727]
[ 0.] [ 1.23691279e-10] [ 0.]
[-92.79470071] [-92.79467095] [-92.79470071]
[ 2383.66211583] [ 2383.66209637] [ 2383.66211583]
[-10725.22892185] [-10725.22889937] [-10725.22892185]
[ 234.77560283] [ 234.77560254] [ 234.77560283]
[ 4739.22119578] [ 4739.22121432] [ 4739.22119578]
[ 43640.05854156] [ 43640.05848841] [ 43640.05854157]
[ 2592.3866707] [ 2592.38671547] [ 2592.3866707]
[-25130.02819215] [-25130.05501178] [-25130.02819515]
[ 4966.82173096] [ 4966.7946407] [ 4966.82172795]
[ 14232.97930665] [ 14232.9529959] [ 14232.97930363]
[-21621.77202422] [-21621.79840459] [-21621.7720272]
[ 9917.80960029] [ 9917.80960571] [ 9917.80960029]
[ 1355.79191536] [ 1355.79198092] [ 1355.79191536]
[-27218.44185748] [-27218.46880642] [-27218.44185719]
[-27218.04184348] [-27218.06875423] [-27218.04184318]
[ 23482.80743869] [ 23482.78043029] [ 23482.80743898]
[ 3401.67707434] [ 3401.65134677] [ 3401.67707463]
[ 3030.36383274] [ 3030.36384909] [ 3030.36383274]
[-30590.61847724] [-30590.63933424] [-30590.61847706]
[-28818.3942685] [-28818.41520495] [-28818.39426833]
[-25115.73726772] [-25115.7580278] [-25115.73726753]
[ 77174.61695995] [ 77174.59548773] [ 77174.61696016]
[-20201.86613672] [-20201.88871113] [-20201.86613657]
[ 51908.53292209] [ 51908.53446495] [ 51908.53292207]
[ 7710.71327865] [ 7710.71324194] [ 7710.71327865]
[-16206.9785119] [-16206.97851993] [-16206.9785119]
As you can see normal equation, least squares and np.linalg.solve tool methods give to some extent different results. The question is why these three approaches gives noticeably different results and which method gives more efficient and more accurate result?
Assumption: Results of Normal equation method and results of np.linalg.solve are very close to each other. And results of np.linalg.lstsq differ from both of them. Since normal equation uses inverse we do not expect very accurate results of it and therefore results of np.linalg.solve tool also. Seem to be that better results are given by np.linalg.lstsq.
Upd:
As Dave Hensley mentioned:
After the line np.fill_diagonal(IdentityMatrix, 1)
this code IdentityMatrix[0,0] = 0 should be added.
DB2.csv is available on DropBox: DB2.csv
Full Python code is available on DropBox: Full code